Nerd Sniped - Solving for Jumbles and Letter Boxed
tl;dr
I got nerd sniped by a problem and wrote a solver for it. You can find it here.
The Problem
Apparently it’s impossible to determine if someone is capable of coding without asking them arbitrary puzzles that are in no way related to a realistic job. Resumes and previous job experience are so passe - puzzles are where it’s at.
I received one of these coding challenges - given a jumble of letters, find all possible words you could spell. While annoying that I had to do it in the first place, it did manage to nerd snipe me a little bit. Then I realized an interesting twist would be to modify it for a game I actually played most mornings; Letter Boxed.
Jumble Solving
First let’s look at the initial, easier problem - Jumble solving. Given a set of letters, find all possible words that can be spelled with those letters. This is a twist on a more classic problem, wherein the candidate is typically asked to find all possible anagrams of a given subset of words - ie dog → god, dog, gdo, etc. This is quite easy in comparison - you don’t actually need to do much searching. You can preprocess your wordlist by scanning through, ordering the letters, and then storing the word within a hash table wherein the key is the ordered letters of the word and the value is a list of possible matches. Similarly sorting the anagram word to check would allow an O(1) scan time to read back the list of possible matches, an O(n) space complexity (with n being our wordlist size) as you’re storing the wordlist in memory, and an O(n) time complexity to preprocess the wordlist. Easy peasy.
…but once you ask for smaller words, and don’t allow letter reuse - that’s when the problem becomes a real search problem. I created two solutions.
The Simpler Scan Method
In this method, the user chooses the word list to scan against and the letters in the jumble. We then do the following
- Prepare a count of letters within the jumble stored as a
dict- the key is the letter and the value is our count. We will refer to this ascount - Load and process through the given word list. For each word, scan through each letter. If the letter is not in the
countdict, the word can’t be spelled with the jumble. If it is incount, we then check the current count value of the given letter. If it’s greater than0, decrement it and move onto the next letter. Otherwise the word can’t be spelled with the jumble. If we go through all possible letters of the word, congratulations; the word can be spelled with the jumble.
Space complexity is O(1) (we only need the jumble letters transformed to a count) and the time complexity is O(n*m) where n is our wordlist and m is the maximimum word size. Since we’re probably not concerning ourselves with absurd length words it’s probably to just call it O(n) unless we’re being pedantic.
The downside to this approach is that if the wordlist doesn’t change regularly you’re paying a large cost on each search for each jumble checked. If we were creating a service specifically to solve jumbles with a rarely changing wordlist we could probably find a more efficient way, right?
The Trie Method
A trie is a specific type of tree structure - it is a tree where each node represents a letter. The structure of the tree represents words, and the children of each letter represents the next letters in the spelling of words.
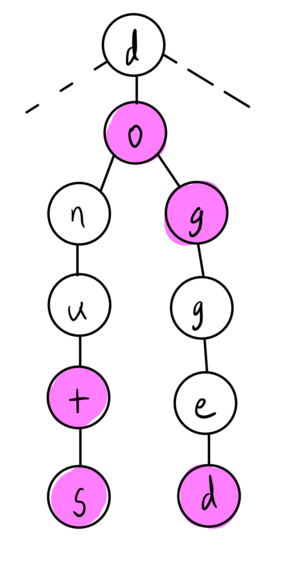
One additional common trait of a trie is a terminator attribute; you may have children nodes, but the given letter may still spell a smaller word. Consider dog and dogged - the first g terminates a known word, but can still be further explored.
A slight optimization ignored
There is one slight improvement you can do to a trie structure I didn’t explore here - compressing the trie to allow a more DAG (Direct Acyclic Graph) structure. The quickest explainer is to observe these two different approaches:
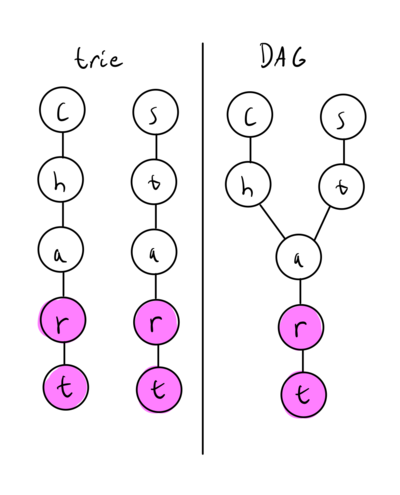
Once you form the trie, you can go back through and “compress” the tree to a DAG allowing some benefits to space complexity. I don’t know off the top of my head, but I suspect there is also additional searching benefits wherein you can search backwards in such a structure. I leave that to the motivated reader.
Code
Let’s start diving into some code. First we’ll look at the simpler scan method. We have our core function - given the word and the path to our wordlist, solve the jumble.
def jumble_solve(filename: str, base_word: str) -> List[str]:
"""
jumble_solve scans through the given wordlist and
determines what words are possible out of it. It
solves the jumble while loading the word list as
opposed to my other solution, which creates a
reusable graph approach. For single use or longer
jumbles, this is faster.
"""
# Get base letter count
base_letters = build_base_letter_count(base_word)
# Load our word list
words: List[str] = []
with open(filename, "r") as file:
reader = csv.reader(file)
for row in reader:
word = row[0]
# Note - dict({}) is a performant way to copy a
# shallow dict, since we don't want to actually
# modify the count in our scoped base_letters
if word_composition_check(dict(base_letters), word):
words.append(word)
return words
…then we have the function to quickly build our letter count.
def build_base_letter_count(word: str) -> dict[str, int]:
"""
build_base_letter_count builds a dictionary of letters
and their counts from a given word.
"""
letter_count: dict[str, int] = {}
for letter in word:
if letter in letter_count:
letter_count[letter] += 1
else:
letter_count[letter] = 1
return letter_count
…finally we have our check for the word composition.
def word_composition_check(base_letters: dict[str, int], word: str) -> bool:
"""
word_composition_check confirms that a given word can
be formed from letters within the base word, without
letter re-use. Smaller words are allowed.
This is accomplished by moving through the word list and
comparing it to the base letters count dict. If the letter
from a word X is not in the dict, then the word cannot
exist; return False. If the letter is in the dict,
decrement the count. If the count is less than 0, we have
used that letter too often and thus the word cannot exist;
return False. If we make it through this process, then the
word must be possible with our available letters, and we
return True.
"""
for letter in word:
if letter not in base_letters:
return False
else:
base_letters[letter] -= 1
if base_letters[letter] < 0:
return False
return True
One thing to note - why am I wrapping the base_letters dict in dict() in our core search function? It’s essentially quickly cloning the dict when passing it in - the act of marking letter as “used” in the search would modify the base dict if we didn’t do this.
The results - pretty flat. The time complexity is, as you’d guess, O(n), with only slightly more time utilized for longer and longer jumbles.
| Letters | Time |
|---|---|
| 1 | 0.30149 seconds |
| 2 | 0.28906 seconds |
| 3 | 0.30319 seconds |
| 4 | 0.30238 seconds |
| 5 | 0.32480 seconds |
| — | — |
| 30 | 0.49711 seconds |
| 31 | 0.49912 seconds |
| 32 | 0.52220 seconds |
| 33 | 0.49713 seconds |
| 34 | 0.50754 seconds |
…and if you’re wondering why 34 letters… well, supercalifragilisticexpialidocious was my test letter set, of course.
The Trie method
Now onto the trie method. I’ll be using classes to create clear readable code - which isn’t as efficient as say, tuples or some other primitives - focused approach; but if your goal was pure speed efficiency you wouldn’t be using Python.
Let’s express each node of the trie as a class
class LetterNode:
def __init__(self, letter: str, terminal: bool = False):
self.letter = letter
self.terminal = terminal
self.nodes: Dict[str, LetterNode] = {}
A very simple start - the assigned letter it represents, whether or not this specific node represents a termination of a word, and its children nodes, represented as a dict where the key is the letter and the node its value for O(1) lookup.
We’ll need a way to add children easily and correctly:
def add(self, node: LetterNode):
"""
add appends a node to our current node
"""
self.nodes[node.letter] = node
While my trie construction method should properly mark a node as terminal when it’s a word, we should consider other construction methods in the future being less explicit. We should consider, for safety, a lack of children nodes being terminal as well. A quick helper function handles this:
def word(self) -> bool:
"""
word returns if a node is demarcated as a word;
nodes can be marked as such if it's a leaf node
*or* if it's a marked "terminal", aka the end of
a smaller word ie: sad->sadder - sad is a word
despite not being a leaf node, as many words
build off of those three letters.
"""
return len(self.nodes) == 0 or self.terminal
We might as well keep it organized, and use our recursive function as a function of the class itself. We start with a given set of letters and call the head node. For each letter, we check the associated child node (if one exists) and then call the search function for that node with the other letters, reducing our search space over time. If a terminal node is hit, we append the possible results with that letter, continue the search amongst its children, and finally return a set of “words” - which are really word fragments.
As that list is returned back up the trie, we append the current node’s assigned letter to the word fragments, essentially spelling the word backwards. The final return - the first function we called, will thus be a list of words that can be spelled with the given letters.
An example - if our trie path went through r→o→b→o→t, the return process would be t→ot→bot→obot→robot.
Since we want a singular entry point, the head node will be a blank string so it can search all letters in our jumble without adding anything to the returned words.
def search(self, letters: List[str]) -> List[str]:
"""
search accepts a set of letters and then performs a query
down our node's branches for words that utilize those
letters. To do this, we traverse each possible letter
combination recursively. Every time we meet a terminal
(leaf or demarcated terminal) node, we have found a word.
We then return up the recursive chain to form the words
discovered throughout our burrowing.
"""
words: List[str] = []
# If our current node is marked as a word, we can return
# that portion of the word from just this node
if self.word():
words.append(self.letter)
# We iterate through each letter available as our
# next target levels through the tree
for index, letter in enumerate(letters):
current_node = self.get(letter)
# If the current node does not exist, we must
# skip it as there is nothing more to search
if current_node is None:
continue
# Ignoring our current letter, isolate all remaining
# letters
remaining_letters = letters[:index] + letters[index + 1 :]
# Search the current target node with the remaining
# letters
found_words = current_node.search(remaining_letters)
# Combine words if any were returned with the current
# node's letter.
for word in found_words:
word = self.letter + word
if word not in words:
words.append(word)
return words
Most of the heavy lifting is done here. To make life a bit easier, we still need to create the functionality for generation and management of the trie.
class JumbleSolver:
def __init__(self, wordlist: Optional[List] = None):
# Our word graph is initiated with a blank letter
# so we can just branch off of that when searching
self.word_graph = LetterNode("")
if wordlist is not None:
for word in wordlist:
self.add_word(word)
def add(self, word: str):
"""
add_word appends a word to our internal tree graph
of possible words.
"""
letters: List[str] = list(word)
current_node = self.word_graph
for letter in letters:
# If we have a node for this letter
# already, utilize it
node = current_node.get(letter)
# If not, create a fresh node
if node is None:
node = LetterNode(letter)
current_node.add(node)
# ...and continue onto the next letter
current_node = node
# Mark the leaf node as terminal, in case
# another word builds off of it. ie; do->dog
current_node.terminal = True
def search(self, word: str) -> List[str]:
"""
search accepts a word and performs a query across the
tree starting with root node. It returns a list of all
possible words
"""
return self.word_graph.search(list(word))
@staticmethod
def LoadFromFile(filepath: str) -> JumbleSolver:
with open(filepath, "r") as file:
solver = JumbleSolver()
reader = csv.reader(file)
for row in reader:
word = row[0]
# Clean the word just in case; limit to lowercase
# and eliminate spaces.
word = word.strip().lower().replace(" ", "")
solver.add(word)
return solver
Results
The results of this method started promising. A quick test of a 5 letter jumble took a fraction of a second to find all possible words - something that took a half second (an amount of time a human can actually notice) to occur. Large and larger jumbles started to show a bit more lag, however.
By my best estimation, this method still has O(n) space complexity (we’re storing the trie in memory, and thus grows with the word list) but O(n!) time complexity. The key difference is that our n in this time complexity case grows off the size of our jumble, not the size of the word list. It grows in complexity because we perform a search across each letter combination, and for each of those searches we perform an additional search for each remaining letter, then by each of those remaining letters, etc.
…but, because it’s based off of the jumble size, even with the worse time complexity we can achieve better performance to a point. If you try a jumble too large, well… let’s look at the results:
| Letters | Time |
|---|---|
| 1 | 0.00004 seconds |
| 2 | 0.00006 seconds |
| 3 | 0.00015 seconds |
| 4 | 0.00023 seconds |
| 5 | 0.00072 seconds |
| 6 | 0.00124 seconds |
| 7 | 0.00324 seconds |
| 8 | 0.00723 seconds |
| 9 | 0.02566 seconds |
| 10 | 0.03621 seconds |
| 11 | 0.05425 seconds |
| 12 | 0.10192 seconds |
| 13 | 0.14558 seconds |
| 14 | 0.27253 seconds |
| 15 | 0.37936 seconds |
| 16 | 0.60944 seconds |
| 17 | 0.95953 seconds |
| 18 | 2.08020 seconds |
…we can see that once we get around 15 letters we’re matching or exceeding the time it took for our prior scan method to simply go through the list and check each word. As you’d expect, it gets significantly worse fast.
| Letters | Time |
|---|---|
| 16 | 0.60944 seconds |
| 17 | 0.95953 seconds |
| 18 | 2.08020 seconds |
| 19 | 3.25990 seconds |
| 20 | 5.21902 seconds |
| 21 | 9.40229 seconds |
| 22 | 10.6053 seconds |
| 23 | 17.1072 seconds |
| 24 | 26.1821 seconds |
| 25 | 45.5737 seconds |
| 26 | 72.0461 seconds |
| … | … |
| 34 | 2444.35706 seconds |
Yeah - supercalifragilisticexpialidocious takes 40 minutes to solve! Where a!<b, wherein a is our jumble size and b is our wordlist size, the trie method will outperform the scan method albeit with worse space complexity.
If you were building this as an actual service you’d have to decide your domain of usage; or just check the wordlist size and jumble size and choose accordingly.
Another ignored optimization
One thing to note - both of these solutions could be parallelized pretty easily. The scan method can have multiple threads, each with its own subset of the wordlist. The trie can, once generated, be accessed by multiple threads, each assigned some combination of letters to search for.
Letter Boxed
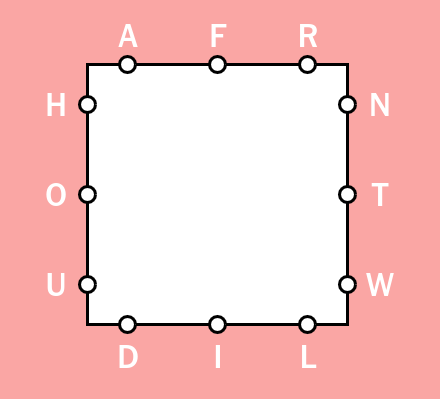
Wordle briefly took over the world and managed to cement itself as a nice little morning ritual for myself and my wife; one where we see who could solve the puzzle in the fewest guesses. One game that briefly joined it was Letter Boxed, also served on the New York Times game page.

The game: you are provided a square with three letters a side. You must utilize all letters in as few words as possible; while letters can be reused, you can not use the same “edge” of the square twice in a row. Similarly, the proceeding word must start with the last letter of the previous word. The puzzle challenges you to solve within typically four to six words, depending on the difficulty.
Annoyingly, the web site doesn’t give me what the optimal solution should have been. I prided myself on usually getting it within three words (granted after hours of passively and occasionally tinkering on solutions), but how much better could the answers be?
Encoding our problem
We now have a new structure with its own rules to encode. A quick use of named tuples to describe our game:
class Edge(NamedTuple):
a: str
b: str
c: str
class Puzzle(NamedTuple):
left: Edge
right: Edge
top: Edge
bottom: Edge
def __str__(self):
puzzle = f" __{self.top.a}__{self.top.b}__{self.top.c}__ \n"
puzzle += f"{self.left.a}| |{self.right.a}\n"
puzzle += f"{self.left.b}| |{self.right.b}\n"
puzzle += f"{self.left.c}|__________|{self.right.c}\n"
puzzle += f" {self.bottom.a} {self.bottom.b} {self.bottom.c} \n"
return puzzle
…with a __str__ method to print the puzzle all pretty like:
__a__t__k__
l| |h
u| |r
n|__________|i
f e s
The trie method
I dove into modifying the trie method for our new problem. Loading the wordlist changes very little, but we do need to modify the search function to deal with our new game rules:
def search(
self, puzzle: Puzzle, current_edge: Optional[Edge] = None
) -> List[Tuple[str, Edge]]:
"""
search accepts a given puzzle, the current edge (which can
be None for the initial start) and returns a list of all
possible words that can be spelled with the available
letters of the puzzle.
"""
search_results: List[str] = []
# If our current node is marked as a word, we can return
# that portion of the word from just this node
if self.word():
search_results.append((self.letter, current_edge))
# Isolate the next edges we can choose from
if current_edge is not None:
next_edges = [edge for edge in puzzle if edge != current_edge]
else:
next_edges = puzzle
# For each edge choose-able we can select a single letter
# from each of the remaining edges at a time. So for each
# edge we choose each letter, searching with that as our
# current_edge
for edge in next_edges:
for letter in edge:
current_node = self.get(letter)
if current_node is None:
continue
results = current_node.search(puzzle, edge)
# Combine words if any are returned with the current
# node's letter
for result in results:
word = self.letter + result[0]
last_edge = result[1]
search_results.append((word, last_edge))
return search_results
We consider each edge, excluding the current from the search space (the current edge is null for the start of our search). This enforces the game rule of not repeating letters from the same edge.
We keep track of the last edge used within the word too since we have to start the next word from that point. We can’t just check the last letter of the word, since the letter could appear on multiple edges.
Moving onto our solver to contain the trie and perform the higher level of our search:
class LetterBoxedSolver:
def __init__(
self,
wordlist: Optional[List] = None,
):
# Our word graph is initiated with a blank letter
# so we can just branch off of that when searching
self.word_graph = LetterNode("")
if wordlist is not None:
for word in wordlist:
self.add_word(word)
def add(self, word: str):
"""
add_word appends a word to our internal tree graph
of possible words.
"""
letters: List[str] = list(word)
current_node = self.word_graph
for letter in letters:
# If we have a node for this letter
# already, utilize it
node = current_node.get(letter)
# If not, create a fresh node
if node is None:
node = LetterNode(letter)
current_node.add(node)
# ...and continue onto the next letter
current_node = node
# Mark the leaf node as terminal, in case
# another word builds off of it. ie; do->dog
current_node.terminal = True
@staticmethod
def LoadFromFile(filepath: str) -> LetterBoxedSolver:
with open(filepath, "r") as file:
solver = LetterBoxedSolver()
reader = csv.reader(file)
for row in reader:
word = row[0]
# Clean the word just in case; limit to lowercase
# and eliminate spaces.
word = word.strip().lower().replace(" ", "")
solver.add(word)
return solver
Here we have a similar setup from before - store a wordlist, and have a function to add words to the trie, and a helper function to read from a CSV file a word list. Then we need to add a search function to handle solving our puzzle with the trie, handling puzzle logic as well:
def search(self, puzzle: Puzzle) -> List[List[str]]:
complete_list: List[List[str]] = []
in_progress_lists: List[List[Tuple[str, Edge]]] = []
current_list: Tuple[List[str], Edge] = ([], None)
puzzle_solutions: Dict[str, bool] = {}
while True:
current_words = current_list[0]
current_edge = current_list[1]
if len(current_words) == 0:
node = self.word_graph
else:
last_letter = current_words[-1][-1]
node = self.word_graph.get(last_letter)
results = node.search(puzzle, current_edge=current_edge)
if results is None and len(in_progress_lists) == 0:
break
elif results is None:
current_list = in_progress_lists.pop(0)
continue
for result in results:
word = result[0]
edge = result[1]
# Avoid repeat words in the same chain
if word in current_words:
continue
word_list = current_list[0].copy()
word_list.append(word)
leaf = [word_list, edge]
if self.are_all_letters_used(puzzle, word_list):
# Perform a duplicates check to ensure that
# some combination of other edges aren't
# reported as a unique answer - while it would
# be, we don't report edges in our solver
# so it would look like a duplicate. This would
# occur in some scenarios where a letter is
# duplicated on multiple edges.
smashed_words = "_".join(word_list)
if smashed_words not in puzzle_solutions:
complete_list.append(leaf)
puzzle_solutions[smashed_words] = True
else:
in_progress_lists.append(leaf)
# If we have no more in progress lists, we're done!
if len(in_progress_lists) == 0:
break
current_list = in_progress_lists.pop(0)
# Now that we have the list, limit it to just the words,
# and let's sort it by lowest amount of words, with the
# least number of letters leading.
complete_list = [leaf[0] for leaf in complete_list]
complete_list.sort(key=lambda x: (len(x), sum([len(word) for word in x])))
return complete_list
We take a given puzzle and begin searching with a null current_edge. We track completed words within complete_list. Chains of words that are achievable within the puzzle but are not yet utilizing each letter of the puzzle are stored as in_progress_lists. The are_all_letters_used function checks if the given words_list generated utilizes all of the letters or not.
When a word is returned and the next in the chain is searched, we used the LetterNode’s returned edge from its search function to ensure that the next word starts not just with the last letter but originates from the last edge as well.
This seemed good to me. I ran it and, after a few quick bug fixes, let it run. …and run. …annnnnnd run.
What was happening? Checking with a debugger showed that it was generating words that followed the rules; but it was finding a lot of words. Even after several minutes, the in_progress_lists grew rapidly.
It dawned on me that the jumble search space was limited because letters were not allowed to be reused. The search space here is much larger since it allowed letter reuse.
To see if I could find a solution reasonably, I tried adding an iteration limit - once the solver tried processing a set amount of solutions just abort.
This worked, but didn’t reliably provide great solutions. I found most of my solutions fell into the three or two word space - which is good - but because of the huge search space I was likely missing the best solution.
What if I modified the solver’s search function to limit not by iteration, but by answer length? I could tell it to reject any possible chain of solutions that would require more than two or three words to solve, greatly reducing my actual search space.
if self.are_all_letters_used(puzzle, word_list):
# Perform a duplicates check to ensure that
# some combination of other edges aren't
# reported as a unique answer - while it would
# be, we don't report edges in our solver
# so it would look like a duplicate. This would
# occur in some scenarios where a letter is
# duplicated on multiple edges.
smashed_words = "_".join(word_list)
if smashed_words not in puzzle_solutions:
complete_list.append(leaf)
puzzle_solutions[smashed_words] = True
else:
# If we limit the chain size, aka how many
# word solutions we'll accept, then we
# check here if we'll have to match or
# exceed that don't even consider it.
if self.max_chain > -1:
if len(word_list) < self.max_chain:
in_progress_lists.append(leaf)
else:
in_progress_lists.append(leaf)
This worked. Trying the puzzle above with a limited solution size of three words:
__a__t__k__
l| |h
u| |r
n|__________|i
f e s
Possible answers: 441298
Took 5719.42503128377 seconds
Top ten answers:
1 - ['urns', 'shaftlike']
2 - ['hants', 'surflike']
3 - ['hasnt', 'turflike']
4 - ['futharks', 'sline']
5 - ['futharks', 'silen']
6 - ['surflike', 'ethan']
7 - ['shant', 'turflike']
8 - ['lanternfish', 'huk']
9 - ['laft', 'tinkershue']
10 - ['ruins', 'shaftlike']
It worked, finding 441,298 solutions, but took a damned long time - 95 minutes! Plus the top solutions are all two words, which means we’re spending a lot of time searching for three word solutions when two will suffice.
Re-running the same puzzle allowing just a search space of two words:
__a__t__k__
l| |h
u| |r
n|__________|i
f e s
Possible combos: 441
Took 20.10149908065796 seconds
Top ten answers:
1 - ['urns', 'shaftlike']
2 - ['hants', 'surflike']
3 - ['hasnt', 'turflike']
4 - ['futharks', 'sline']
5 - ['futharks', 'silen']
6 - ['surflike', 'ethan']
7 - ['shant', 'turflike']
8 - ['lanternfish', 'huk']
9 - ['laft', 'tinkershue']
10 - ['ruins', 'shaftlike']
This found just 441 solutions and took a mere 20 seconds. Much better.
Since we’re allowing letter re-use the O(n!) from the jumble trie search becomes O(n^n) here! This explains the exploding search time from our previously successful jumble solver; the jumble solver and Letter Boxed both have 9 letters to work with, but the search spaces differ by several orders of magnitude:
…which is per search, of which the Letter Boxed solver has to do for each found solution, actually making it O((n^n)^m) where m is our possible valid words. Actually, it might be worse if we consider that the search space expands past two words. I’m not sure how to calculate that. This explains the time difference between the Jumble’s 9 letter 0.026 second search and our much slower searches requiring search space limitations.
We could implement another optimization here to help; two actually. The first is to not hard limit the search space, but allow the searcher to be cognizant of the smallest completed solution, and limit the search space to that alone. This is a lot of effort considering that the best solution seems to always be two words.
The second optimization would be to also consider the length of discovered solutions' words. If that length was passed into active searches of the trie we could abort the search of words earlier once we reach a the best known length, drastically reducing search space.
The scan method
I originally though you couldn’t do a scan method for this problem since you need to branch consecutive words together, implying that a solution would be an O(n^n) search wherein n is our wordlist size. But, if we know the best solution is always going to be two words anyway, we can cheat.
We can scan through a given word list, noting what words are “valid” and can be spelled with our given puzzle rules. Once we do that, we can store them in a dictionary where the key is the first letter of their word. This first pass greatly limits our search space for the second step.
Now, for each letter in our dictionary, we scan through all valid words that started with that letter. We take the last letter of each of these words and then grab each word that starts with that letter. We can do a quick and computationally cheap check - does the prior word and this one complete the puzzle? If not ignore it; otherwise it’s a solution.
def solve(puzzle: Puzzle, wordlist: List[str]) -> List[List[str]]:
solutions: List[List[str]] = []
# valid_words is a alphabet delimited list of words that
# are valid; this is used to limit the search space
# on our second word search
valid_words: Dict[str, List[str]] = {}
for word in wordlist:
if not word_composition_check(word, puzzle, None):
continue
if word[0] not in valid_words:
valid_words[word[0]] = []
valid_words[word[0]].append(word)
# Now scan through all words in valid_words for the
# second word to try and solve the puzzle
for letter in valid_words:
for word in valid_words[letter]:
last_letter = word[-1]
if last_letter not in valid_words:
continue
for next_word in valid_words[last_letter]:
if next_word == word:
continue
if are_all_letters_used(puzzle, [word, next_word]):
if solutions.count([word, next_word]) == 0:
solutions.append([word, next_word])
solutions.sort(key=lambda x: sum([len(word) for word in x]))
return solutions
Not nearly as elegant; but does it run well?
__a__t__k__
l| |h
u| |r
n|__________|i
f e s
Possible answers: 441
Found 441 solutions in 8.104941129684448 seconds.
Top ten answers:
1 - ['urns', 'shaftlike']
2 - ['hants', 'surflike']
3 - ['hasnt', 'turflike']
4 - ['futharks', 'sline']
5 - ['futharks', 'silen']
6 - ['surflike', 'ethan']
7 - ['shant', 'turflike']
8 - ['lanternfish', 'huk']
9 - ['laft', 'tinkershue']
10 - ['ruins', 'shaftlike']
Not only is this approach simpler, but it’s faster too. Damn; the trie solution was cooler and I was hoping it’d be the winner. Though this method does completely break down if we expand it past two word solutions; though it seems the trie method’s search space similarly becomes restrictive.
Wordlists and solutions
One common problem I encountered were words my word list contained that the New York Time’s game rejected as valid. I had compiled my wordlists from a few random sources and wanted to refine it to the master wordlist provided by the New York Times. Unfortunately I couldn’t find any official list hosted online through Kagi or GitHub.
I jumped onto the Letter Boxed game site and opened the network page. Submitting a word to be checked didn’t fire off a network request, so we were definitely loading the word list locally. I scanned through existing variables on the window and found gameData.
Here I found two interesting tidbits. The first is that the New York Times does provide their preferred “best” answer within gameData.ourSolution, but doesn’t show it to the player for some reason.
The next is that they pre-filter the wordlist to words that are possible within the puzzle within gameData.dictionary; a list of only a few hundred words per day. Thus it would take weeks of watching the game to compile a mostly complete wordlist.

Conclusion
All the code for this post can be found here.
A fun little nerd sniping; I think I’m done with it for now. Is there a quicker way to approach this problem? Let me know if so.