Diffusion Models Are Real-Time Game Engines
Google Deepmind recently released Diffusion Models Are Real-Time Game Engines [Site] | [Paper], a fascinating paper wherein a modified Stable Diffusion model acts as the game engine for the classic game of DOOM. Player actions are fed directly into the model (which they called GameNGen), which outputs a generated image of the next frame 20 times a second. The game state and display is entirely handled by the model itself.
So how did they build it? What can we learn from it? Let’s dive in.
I also covered this paper for a paper club via SDx - feel free to check out the slides here or the presentation below:
A Bird’s Eye View
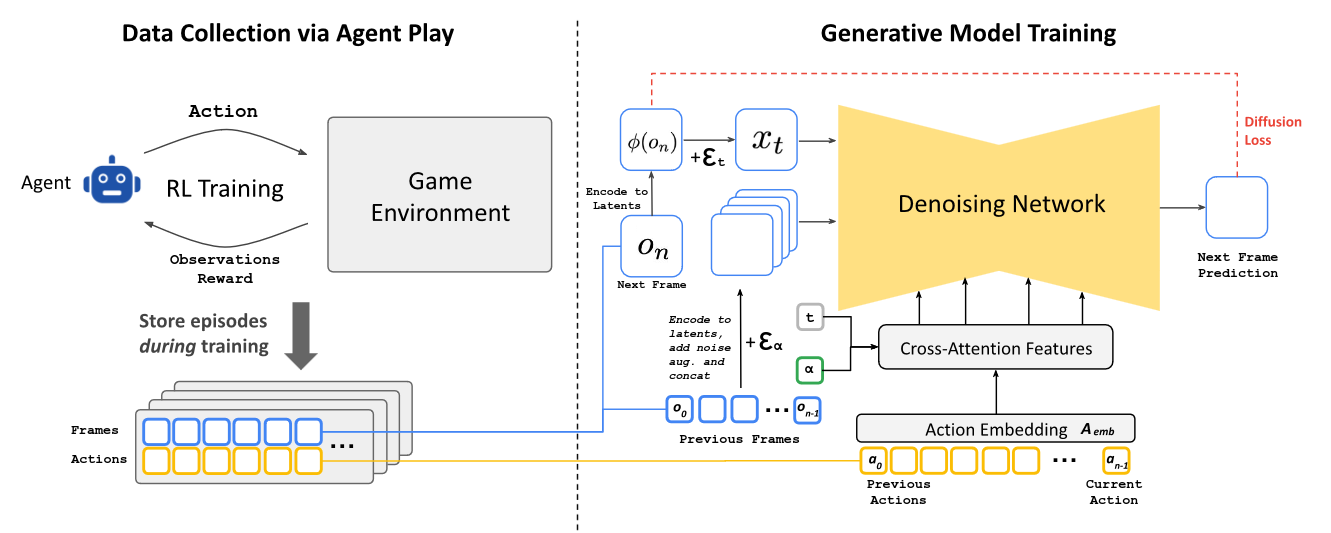
Here’s the architecture diagram ripped from the paper. The right column contains our diffusion network - the engine for our frame generation. But how do we generate the training data for such a network? For that, we first look at the left column - our reinforcement learning agent.
The Agent
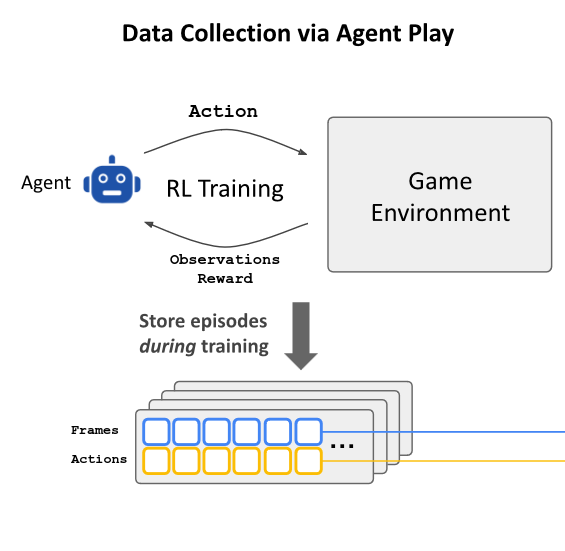
In order to train a diffusion model, we need a lot of images. To generate that dataset, we need to compile a significant amount of frames of DOOM. This isn’t scalable with human players, so the authors created an agent to play the game for them to generate essentially infinite frames as needed.
They followed the general structure of the agent used in Human-Level Control Through Deep Reinforcement Learning - a paper focused on simpler Atari games. It demonstrated an effective agent using the PPO algorithm (more on this in a bit) using convolutional neural nets consuming each frame of the game as the model’s input. The GameNGen model is fed a 160x120 pixel image of the frame into the first convolutional layers; the past 32 actions are additionally fed into the fully connected layers. The output of the network is a probability distribution of possible output actions the agent should take.
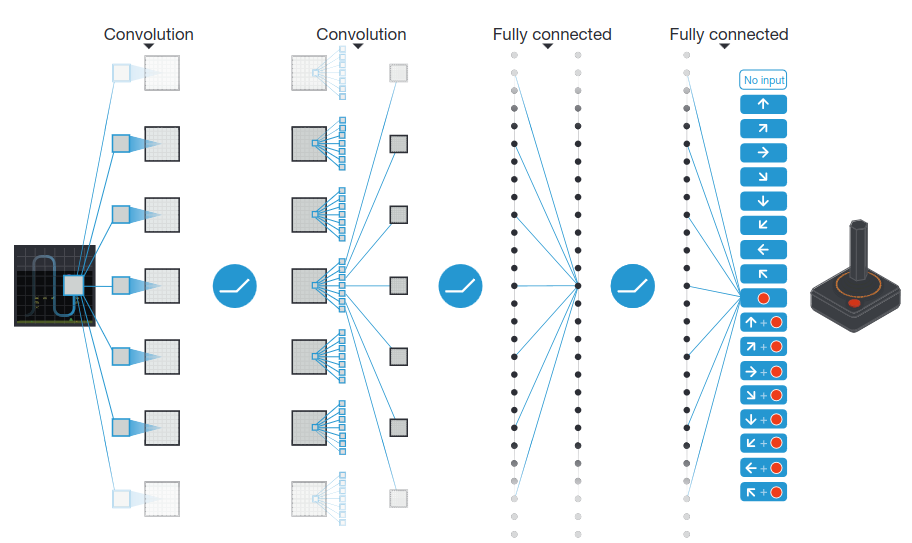
PPO, Briefly
To train, they utilized Proximal Policy Optimation - PPO, released by OpenAI in 2017. PPO is an actor-critic reinforcement learning algorithm for training agents. It’s been the go-to state of the art algorithm for RL training for awhile, and has been powering several fun papers in the past few years:
Learning Dexterous In-Hand Manipulation

OpenAI’s disbanded robotics team (which did some incredible work!) used PPO to create high performance reinforcement learning controled robotic hand to perform complicated in-hand dexterous tasks.
You can see one of the authors, Alex Paino, discuss the project here, and see Open AI’s demos here.
OpenAI Five
OpenAI used PPO to train its agents for DOTA2, forming a five agent team that outplayed some of the best human players in the world. They created a blogpost on their approach talking at a high level how they differed their normal approach to PPO. You can see OpenAI’s video about the accomplishment or watch the gameplay; I’m more of a League victim player so I don’t quite follow the subtleties.
Emergent Tool Use From Multi-Agent Autocurricula

This is by far my favorite paper from the OpenAI RL team. They had competing PPO trained agents that, over millions of timesteps, would learn to compete in a complex virtual game of tag, learning not only strategies but how to utilize tools to score better - and even cheat!
You can check out their fascinating video on the subject here and the slides from the presentation I gave on it during my Master’s here.
Back to explaining PPO
PPO’s biggest advancement was a new way to update models while curtailing large changes to the model’s weights. Since it’s an actor-critic model, we have two models. Our actor is a model that receives the environment state as an input and outputs a set of actions for the agent, acting as our policy Ⲡ. Simultaneously we are training a critic model to evaluate the expected value of the agent being in a particular state.
We perform a rollout (let the agent operate in its environment for a set number of timesteps) to create a batch. Take the reward generated during a given episode and calculate the discounted reward for each step (essentially the reward reduced over time for previous steps from the final to encourage efficiency). With this information we’re going to calculate the advantage A.
Q is our measurement of how good a given action is when taken at a given state, and V is our measurement of how good a state can be for the agent - essentially the average of the state. So we’re asking - “How good was this action compared to the average score when we get into this state?"
Once we have this measurement of advantage, we want to calculate the ratio of probabilities, r:
Or, succinctly explained - what was the probability that the current agent would have chosen action a here versus the probability the prior version of the model would have taken action a?
We then perform a min’ed clamped function to get our loss.
So the loss is the minimum value of a clamped ratio of how likely the agent was going to perform the action and how much better (or worse) than average the action was for the model. I have an in-depth post walking through how this can be done in practice here, wherein I used PPO to train a pick and place robotic arm.
The authors utilized Stable Baselines 3 to quickly build and train their network. They kept the training CPU-bound (since rollout takes significantly longer then training and is cheaper). 8 games were ran in parallel with a 512 replay buffer size (reusing experiences from prior batches to enhance batch diversity). The model was trained in 10 million environment steps. were utilized to train the model.
Human-Like Performance
Reward engineering - defining rewards for an agent’s interaction with its environment - is important to get desired behavior out of agents. The authors wanted to a “human-like” experience, so they carefully structured the scoring:
| Event | Score |
|---|---|
| Player hit | -100 |
| Player death | -5,000 |
| Enemy hit | 300 |
| Enemy kill | 1,000 |
| Item/weapon pick up | 100 |
| Secret found | 500 |
| New area discovered | 20 * (1 + 0.5 * L1 distance) |
| Health Δ | 10 * Δ |
| Armor Δ | 10 * Δ |
| Ammo Δ | 10 * max(0, Δ) + min(0, Δ) |
This encouraged the agent to prefer maintaining higher health, not wasting ammo, killing enemies, and not dying - exactly what you’d expect a human player to do if dropped into the game.
Did we even need the agent?
Sort of? For an ablation study the authors utilized a random agent to create a secondary dataset for comparison. The resulting dataset still trained a useable diffusion game engine, but it suffered significantly in certain areas where the random agent rarely or could not reach - secret areas or hard to reach spots. Below we see the performance difference across individual frame comparisons for the random and RL agents - there’s clearly some divergence in what the model is able to represent.
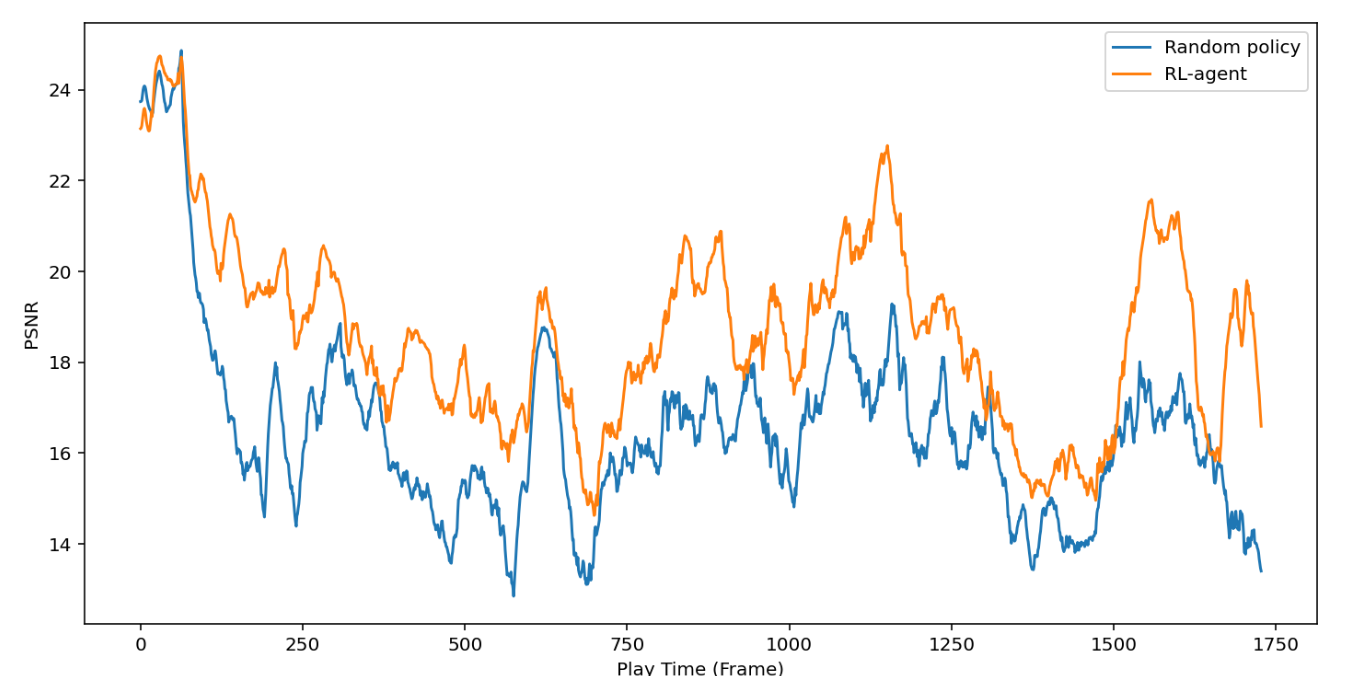
This is in contrast to an interesting point that came up in our paper club discussion of Google Deepmind’s Grandmaster-Level Chess Without Search! One of the attendees asked if the agent demonstrated there would learn grandmaster level chess if the dataset was curated to only be lower ELO players. I posited that since the model is learning the evaluation function of Stockfish versus the actual rules of chess from a behavior cloning approach, that yes, it would still achieve that level of performance if the dataset was large enough. Since we’re actually recreating the state within this model - and the image output is more difficult to reason about than a singular board state (ok, debatably), the model requires significantly more data to faithfully recreate what it’s trying to approximate.
The Diffusion Model
We now have an agent playing DOOM, recording a super-human number of gameplay frames. What’s next? We train the diffusion model.
Diffusion Models, Briefly Explained
Diffusion models are one of those ideas that causes me to do a double take. Is that really how they work? For a fantastic quick dive into how Diffusion works, check out Computerphile’s look into Stable Diffusion and DALL-E - their explanations are always top notch.
The tldr of the process is that we’re not training a model to generate an image directly. Rather, we’re training a model to remove some amount of Gaussian noise from an image with come contextual conditioning (in the form of tokens, representations, other images, etc). The output of the model is repeatedly fed back in until we reach a level of generation we’re happy with. Once trained, we can start with pure noise and slowly, incremently remove noise until we are left with our desired robot riding a unicorn through a nebula while blowing bubbles.

Stable Diffusion
Stable Diffusion’s big advancement was to not work in pixel space (on the images themselves) but rather within a latent space. First you train a Variational AutoEncoder (VAE) - an autoencoder that uses probability distributions as the latent space instead of straight values with additional regularization in the training of the encoder. These are great not just for compressing content into a representation that has some heuristic understanding of what its dataset is, but the probability distributions allow better generation of new outputs in a similar manner. The latent space vectors are significantly smaller than pixel space image data, and thus Stable Diffusion is more efficient.
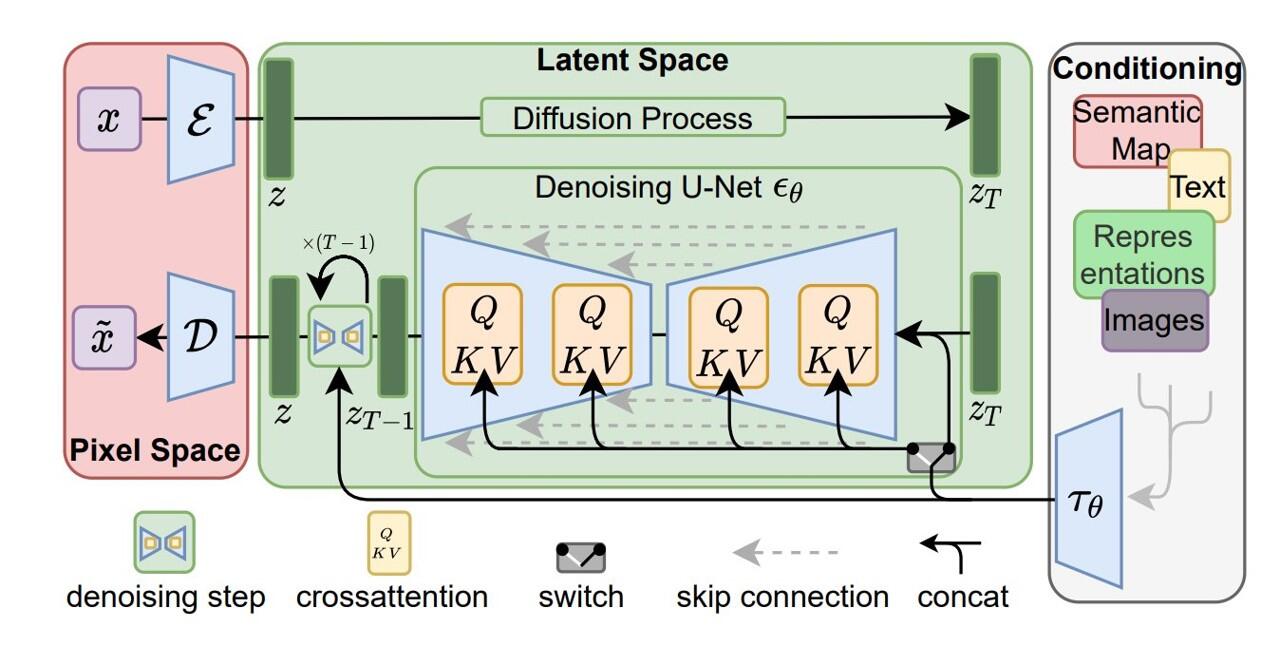
Stable Diffusion and other diffusion networks often use a U-Net style denoising network. U-Nets were originally developed for semantic segmentation (you can see a project where I used it for this in a self-driving car here), but also work great for context aware image editing because its architecture prevents losing information via skip connections.
GameNGen

The authors modified Stable Diffusion to adapt it to their purposes, feeding not just the Gaussian noise latent vector we’re slowly denoising, but also the last n latent vectors/frames (they tested various sizes in their research, but typically it was 64 frames, or about 3 and change seconds). For the conditioning, they used the last 32 actions tokenized. Note that increasing the memory of the model by passing more frames in did improve performance, but only to a point - they suggest a more context-memory efficient model architecture would be required to span much longer, as improvements hit an asymptotic wall.
Autoregressive drift was causing issues with accurate frame generation. Below is an example of every tenth frame of the player standing still over a period of a just a few seconds:
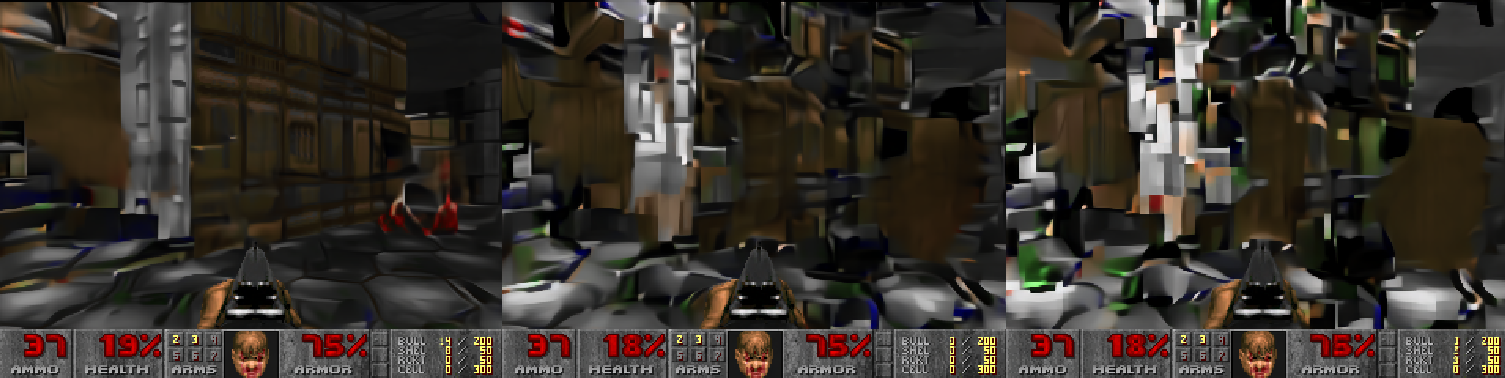
This is similar to covariate shift that you might see in behavior cloning, where even small deviations in practice from the training set causes the agent to begin to drastically veer into increasingly unexpected and thus irrecoverable trajectories - in our case, the frame gets messy quick.
To fix this, the authors implemented an extra step of adding Gaussian noise, to prior frame’s latent spaces when passed in, including the noise level ϵ added to the noise model input (tokenized into bins, which tends to be more stable in training than straight values. We saw this as well in the Grandmaster Chess Without Search paper).
This created significantly improved results - the top row is the model without this technique, the bottom is with:

Results
First, let’s watch someone rip and tear.
There’s more to the results than just demon fraggin' and pixelated explosions; though admittingly that’s a pretty sweet output of a paper. Let’s go over the results.
The biggest claim of the paper is:
Human raters are only slightly better than random chance at distinguishing short clips of the game from clips of the simulation
A bold claim that their engine is essentially barely distinguishable from the real deal. There’s a big asterisk on this though - specifically that word “short” is carrying a lot of weight.
The authors presented a small set of 10 human raters 1.6 second and 3.2 second footage clips of gameplay, both controlled by a human player. Human raters correctly identified the real game-engine gameplay 58% and 60% of the time, respectively.
The paper is still impressive in my mind, but why the shorter clips? Probably due to the ease of observable issues with the short memory of state from the prior frames and actions. Since the model never has more than a bit over three seconds of memory, continuity errors become more obvious on longer timelines. Players could pick up power-ups, move away, then at some point past the memory threshold, turn around and see the power-up incorrectly respawned. Players could find that a newly opened room would contain nothing but dead enemies, as the network’s visual tracking of the state of the player (health, ammo, armor) would suggest to it that the player must have already fought the demons here.
The authors also attempted some numerical benchmarks of similarity. PSNR (Peak Signal to Noise Ratio) is a common measurement of similarity between images and videos when rating compression (higher is better); this model achieved a PSNR of 29.43, roughly in line with a lossy JPEG compression. LPIPS (Learned Perceptual Image Patch Similarity) is another such benchmark (0→1, lower is better); the model achieved 0.249. Similar to aggressive JPEG compression.
These scores tend to drift over time, even on footage that was difficult or impossible to differentiate from the original footage. For a possibly better comparison, they also utilized Fréchet Video Distance (FVD) - a neural network trained metric comparison for video compression. FVD scores 0→1000, with lower values being better. A score of 50 is imperceptible to humans. Here the authors used 0.8 second and 1.6 second long clips, which scored 114.02 and 186.23, respectively. These scores correlate to moderate compression.
Implications
Are games going to be entirely powered by complex neural networks? Of course not. Even ignoring the massive hardware requirements needed (this model required specialized hardware, Google’s TPUv5, to achieve even 20 frames a second), it’s damn near impossible to collect enough gameplay footage to train a model without a completed, working game engine. More complex games - be they through graphical fidelity or complexity of gamestate - will require even more data and complex architectures with better memory. Despite what the sensationalist headlines this paper’s hype generated, game developers aren’t going anywhere anytime soon.
What I’m most excited for is an “understanding of state”. This paper demonstrates what we’ve seen across several works now - for example, my own LLM powered robot, Decision Transformers [Slides], Grandmaster-Level Chess Without Search - there is more cause and effect, a better sense of state management, occurring across attention mechanisms than we’ve seen in earlier machine learning models. We don’t quite understand how the internal mechanisms of transformers are building their world models yet, but we are pushing to new horizons of how we can use it.
I do think we’re going to see additional denoising architectures for simulations as we we develop memory efficient architectures. Once we accomplish this, I suspect we’re in a for a wild ride of new reinforcement learning strategies since sample efficiency and simulation can act as bottlenecks on current approaches.
What do you think? Reach out and let me know.